Lecture 19: Leiserchess Codewalk

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

INSTRUCTOR: So today, we start on project 4, which is, as you know, the big project. And Helen is going to do a walkthrough of the project, and the code, and the organization, because this is a pretty big sized project. It's got about 4,500 lines of code. And it's not code that is kind of like simple code.

It's all content-bearing code. So I think having a bit of an orientation to it, more than we give for the other codes that you work, on which are pretty small, this will be great. So, Helen, take it away.

HELEN XU: Hi, everyone. Can you hear me? Awesome, so today we're going to be doing the walkthrough for the final project. You can look at the code and clone it publicly here. And please remember to fill up your team's by 7:00 PM today, so we can populate the list and get your repos.

Yeah, and if there are any issues accessing this, just let me know. Or put it on Piazza and then we can fix it. So we just had a game of Lesierchess. But in case you missed it, we'll go into more details about what the game actually does.

So first, we're going to go through the game rules. So you saw that there are these pieces. There's these triangles. And there's kings.

So the triangles are pawns. And the kings, they look like crowns. And there are two teams. There's orange and lavender, or tangerine and lavender. And each side starts out with seven pawns and one king.

And this is the starting position. So you can see like the kings are in the corner. And they're just lined up like in the middle. And each piece has four orientations.

So you can see that the pawn is up, down, left, right. And then the king is also like that. And in general, the game starts with tangerine moving first. And then the play alternates between the two players.

Each piece moves the same, whether it's king or pawn. And each turn has two parts. So you saw the demo. But you move first.

When you pick one of your pieces, and you move first. And then at the end, your King has to fire the laser. And the laser reflects off the long edge of the pawn. And they'll kill the pawn if it shoots the short edges.

And one side wins when the king gets shot, or when the opposing king gets shot, whether by themselves or by your own king. And so I talked a little about moving. And at the beginning of each turn, the player to move chooses a piece to move.

And you can move your King or any of your pawns. And there are two types of moves. There's basic moves, and swat moves. And basic moves are just, basically, shifts or rotations.

So in the example, you can rotate 90, 180, or 270 degrees. So in the top, row you just rotate. This is the example of moving a pawn. So you rotate your pawn.

Or you can move to an empty adjacent square. So those are the bottom two rows. And there are eight adjacent squares in this example. So there are eight shifts. But there would be less than eight if you were, for example, like at the edge of the board.

And on a move, you can either shift or rotate. But you can't do both. There are also these swap loops. So if you're adjacent to an opposing piece, you can switch with them. And then you have to make another basic move after that, that is not a swap.

So, basically, you can either-- and it has to be with that same piece that you just swapped with. So you just either shift or rotate. Is everyone good on the rules?

Just a couple more things. So there's this Ko rule, which is from Go, which ensures that the game makes progress. So it makes a move illegal if it undoes the opponent's most recent move by just moving back to where you just were.

So this is an example. Let's say you're tangerine. And you swapped with the purple one right next to you. And then you shifted left and bottom. And so lavender can return by swapping back with your orange piece, and shifting again.

But this is actually, illegal because now you just got to your original position. So you're not allowed to just keep cycling back and forth. And so a draw occurs if there have been 50 moves by each side without a pawn being zapped, the same position repeats itself by the side on move, or the two players agree to a draw.

So just kind of like in chess, a chess clock limits the amount of time the players have to make a move. So you can't just keep competing indefinitely. When it's your moves, your clock counts down.

When it's your opponent's moves, your clock stops. So it's not counting your time. And we used Fisher time control. There's a picture of Bobby Fisher, who made it, up which used an initial time budget and a time increment.

So in this example, there's fis60 and 0.5, which means that, in the beginning, each player has 60 seconds. And you get to use the 60 seconds however you want. And when you end your move, you get 0.5 extra seconds. But the 60 and 0.5 could be anything. That's just an example.

So we'll go into an example of how you actually play this game. For a king to zap the enemy king, it risks opening itself to counter-attack. So look at this example. And how can tangerine zap the lavender pawn in F5, by moving one of its pieces?

AUDIENCE: [INAUDIBLE]

HELEN XU: Move C4.

AUDIENCE: Tangerine, that's lavender.

HELEN XU: You're tangerine in this example. And you're trying to zap the one on F5. Yep?

AUDIENCE: You move the tangerine piece at E22 to F1.

HELEN XU: E2 to F1. Oh, sorry, by zap, it means shoot the backside. That would shoot the long side. Good point.

Yeah, so you're trying to kill the piece on F5.

AUDIENCE: [INAUDIBLE]

HELEN XU: Yeah, exactly. So in this, you can move C2 to B1, as you just said. And then you draw the path. And you can see that you've just killed-- or if you're tangerine, you've just killed the piece at F5.

Now, how can lavender counter? By counter, we mean lavender can win the game from this position.

AUDIENCE: Is it A4 to A3?

HELEN XU: A4 to A3. No, I don't think so. Yep?

AUDIENCE: [INAUDIBLE]

HELEN XU: Sorry, what? King, like the orange one? Oh, the lavender one. You're trying to shoot the orange king.

Oh, yes, you're right. You can, actually. Yes, good, that's not the one that we had, but apparently there are two ways. Good.

So if you notice you could also-- that's another way to get that path. But you can also move one of the pawns. Cool, so this is just pointing out one of the subtleties of the game, which is you should watch out for just naively killing all the pieces you can, because that might open you up to the opponent. Yeah?

AUDIENCE: [INAUDIBLE]

HELEN XU: Yes, it can be from any direction. But the pawns only die if you shoot them from not on the long edge. Yep?

AUDIENCE: What if you shoot your own block?

HELEN XU: By block, you mean your own pawn?

AUDIENCE: Yeah.

HELEN XU: You'll die.

AUDIENCE: Oh.

HELEN XU: Yeah?

AUDIENCE: [INAUDIBLE]

HELEN XU: Yes, but only one piece can be on each square. But you can have as many near you. But do you have a question?

AUDIENCE: Can you make it impossible to kill your person?

HELEN XU: Like your King? Like if you barricaded it by pawns. But then the opponent can come in and swap with them, so it will open your barricade.

AUDIENCE: Can the purple king shoot upward?

HELEN XU: If it wanted to. But then in this example, it would shoot up off the board, and nothing would happen. Yeah?

AUDIENCE: When you kill a pawn, does the laser stop at the place where the pawn is or does it go through the pawn?

HELEN XU: No, it just shoots one. Good questions. Everyone good so far? OK, great.

PROFESSOR: This year, it shoots only one. Last year, it kept shooting.

AUDIENCE: Can the king shoot itself?

HELEN XU: Yes. It should try not to, but it can. So you should be careful.

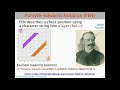
So moving on-- we use force Fosythe-Edwards Notation, which is a representation of a chess position using a string. So you can see an example of the starting position. And the bottom includes the string that describes the starting position.

If you look at the representation, the arrow corresponds to one of the rows. And that points to the substring that has a bubble over it. So in this row, there is one purple pawn at B3, and two orange ones at F3 and G3. So this is row three.

And the slashes separate the rows in the string. And the one represents there's an empty space. And then there's a pawn facing southeast. And then there's three empty spaces, and one facing northwest, and then one facing southeast, and then an empty space.

AUDIENCE: [INAUDIBLE]

HELEN XU: Oh, yeah, it's animated. What do you mean? Yeah, so at the end of the string, there's also a-- it just tells you which side's move it is.

So this is the opening position. But you can use any position in this notation. And this is useful for debugging, because if you, for example, you're running a bot, and it crashes at some position. And you can get back to that position. You can start up the game and just go there without having to make all the moves to get there.

And this is how you represent the games. So each of these is one move. And the left column is tangerine. And the right column is lavender.

And an example, you can see E6, E7, means they moved a piece from E6 to E7. B3L, so you rotated the piece on B3 left. There's D5, E4, F5, which means that you swapped. So your original piece was on D5.

You swapped with the one at E4. And now you moved that piece to F5. So the one that was E4 is now on F5. And the opposing piece is now on D5, because you swapped.

You can swap and then rotate. So instead of just having a third square, you would just have a rotation. And at the end, you could see who won. So in this one, lavender one because it's 0-1. But 1-0 would mean tangerine wins. And half and half would be a draw.

So you can look at the logs for your games. Yes?

AUDIENCE: [INAUDIBLE]

HELEN XU: There's a rotate up and rotate down.

AUDIENCE: [INAUDIBLE] do a U-turn?

HELEN XU: Oh, is that what U is?

AUDIENCE: Yeah, U-turn.

HELEN XU: Oh I, see because there's only three rotations. Yes, sorry, so left is 90. Then right is 270. And U is 180, because you flip it.

Is everyone good on the notation? This is just how you describe the games, if you wanted to look at your logs, and if there are some issues.

So you can test your bot with other teams in the class, as well as with staff bots on the scrimmage server. And we have a reference, which is here, which is just the additional release. But we will be optimizing our bots while we're optimizing your bots.

And we'll release a reference plus, and maybe an even better one later, which you can play with on the scrimmage sever. So I'll just do a really quick demo. So right now, since we haven't done the team formation yet, you are not able to log into this.

But once you do your team formation, probably by tomorrow, you'll be able to log in. And, basically, you can see the general functionality. So this updates your player, pulls your player from your repo, whatever's on the master branch.

And then right now, there's only reference, and reference plus, and reference TAs. And here's a team with me and Jess. But later on, we'll populate this list with everyone in the class. And then you can challenge anybody else in the class to see how you do.

You can also challenge us. So you would just pick, for example, let's say I wanted to challenge reference. And then a hit send challenge.

Now, you can see that there's some new matches spawned. And this is how I look at all the matches that I've played. So each time you hit send challenge, it spawns off two games, one where you're tangerine, and one you're lavender. So that's how you can watch the matches on the scrimmage server.

Everyone good? I'm going to move on so don't run out of town. You can watch them later. And you can even play your own.

OK. And, in addition to the scrimmage server-- so the scrimmage server, you can only spawn off one game at a time. But you can do more.

And you don't have to necessarily do it on your master branch, or against opposing teams in the class. So there's something called the Cloud autotester, which you can run by going to your Athena. And then you type in this command.

You do autotest run. And then you do the time control. And you give it a number of games that you want to run. And then you give it a list of binaries. So I'll go into each of these in more detail.

So the time control is just what I talked about earlier, which is if you use Fisher time control, these are some set, preset things. So you would type in one of the preset things. So you would talk in blitz to do 60 and 0.5, for example.

And the number of games is just whatever you want to do. And the list of binaries-- so let's say you had a reference invalidation, and then you made some change. So I called it Lesierchess with changes.

And then you would just put those after the number of games, separated by spaces. And then it would upload your binaries, and play them in the cloud auto tester. And once you submit your job, you get a link.

And you follow the link in your browser. And you can view the game running. And then after the games are done, you will get some output saying like, which bot, one more? And how many times have won, and some rankings. Yep?

AUDIENCE: How fast do they run?

HELEN XU: How fast do they run?

AUDIENCE: [INAUDIBLE]

HELEN XU: So it depends on how many other games are queued at the same time. So if a lot of people are running tests, it might take some time. But blitz is just how long the game itself will take.

And it might take longer than 60 seconds, because if you use less than 0.5 seconds in your move, and then you add 0.5 seconds at the end of the move, then you would increase your time. But 60 is just the time control.

Each side starts with 60 seconds. And depending on how they use it, they have more or less. Good question.

Well, I'll keep going. And if there's time at the end, I'll do a demo of this one too. But it basically looks the same as the scrimmage server. Like, you just watch the games in the same way.

So now, I'm going to go into the project organization, which is the organization of the directories that we handed out in this repo. So there are some directories. The first one is doc, which just includes the rules and documentation for the interface.

There's the auto tester, which is the Java local auto tester. So if the cloud-- we recommend that you run tests using the cloud auto tester. But if there's some small change, or if you think that-- if the cue is too long, then you can do local tests. And you can also run these overnight.

There's pgnstates, which just parses your statistics from the auto test results, like how many times you won, stuff like that. There's tests, which is how you specify tests. And I'll go into more detail about how you define this.

There's the player, which is where you're actually going to be optimizing. So player is the code that actually runs the bot to play the game. And the webgui is a local webgui where you can watch the game and play it. So in the webgui, you can even play it yourself as a human so you can get a better sense of how the game works.

To go into more detail, the Java local auto tester is an auto tester. You can make your changes, and then you can test your changes. And the test directory, which is parallel, holds configurations. So you can specify the number of games and the bots that you want to use, and the time control, and other things too.

So this an example of the configuration file that you would use to run your auto tester. So this is saying that you run it on 12 CPUs. And book means that you're pointing to open a book, which I'll talk about later.

Game rounds is how many games you're going to spawn off. Title is just the title of the test that you're running. And after that, you have the player definitions. So player reference is just the binary.

And invoke is the path to the binary. And then fis is the time control. And the next one is just a second binary, if you made a change and you want to test them. Yeah, that's the binary.

To interface with auto tester, Lesierchess uses the universal chest interface, or UCI, which is a communication protocol for automatic games. And you pass information between the auto tester and your bot. And it allows the programmer or the auto tester to enter moves to the game engine.

So you could use UCI to start up your bot. And then you type in the moves that you want to make to see the changes in the state. And you could use this to debug to get to a state that you want to look at.

We'll measure the bots using Elo ratings. So Elo is a rating system that measures relative skill level in zero sum games. The Elo rating depends on the Elo rating of your opponents.

And on the bottom, you can see an example output. So I had three binaries. And I ran about 100 games.

And you can see that the Elo of the top one is much higher than the other ones. And so higher Elo is good. And we'll be comparing the performance.

We'll be comparing the Elo of your bot against our reference, and improved reference implementations. So notice that this is not, as before, just a straight measure of time. So like before, in previous projects, if you used less time, than you would get a higher grade or better performance.

In general, I'll show you a graph later that actually shows if you searched the higher depth, which means that you are faster, you do improve. But it's not an exact correlation. And you can look at the nodes per second that you search using the UCI.

And just above here, to local webgui lets you watch a game, or play one, without sending it to the scrimmage server. So if you wanted to play one as a human, you would use the local webgui. And you can run it using the commands in the readme. OK, so is everyone good so far?

Now, I'm going to go into more details about how you actually play the game. So first, every player, or every bot, needs to generate the moves, which means that once you have a position, you need to look at the moves that you can do. And to do that, you need a board representation, which is to represent what pieces are on the board, and how big the board is, and where the pieces are.

And the reference implantation uses a 16 by 16 board to store an 8 by 8 board. So you can see that the inner squares is actually the board. And the outer dark square is sentinels.

So you use sentinels to keep track of when you go off the board. And then the inner square is just the actual board. We store the position using this struct. So you can see the fields in the position, which are the board.

And the array size is just representing the board, plus the sentinels. And there's the history of the position, which is, how did we get here? And there's a key, which is a hash key for this position.

There is ply, which tells you what side it is. So even means white. And odd means black. There is, what was the last move that was made to get to this position?

There's a victim struct, which is the pieces destroyed by when you shot the laser. And there is the location of the kings. The position struct and Lesierchess struct stores the border presentation and other things that I just went through.

So I talked about this move, which means just like a move that you make for one of your pieces. And I'll go into how it's represented. So right now, we already do the packing for you. So we use 28 bits. And the first two are the piece type.

So there's a number of moves that you can make. And the first two bits represents the piece type, which is empty, pawn, king, or invalid. The orientation of the piece, which is just how you rotated it.

The from square, which is where your piece already started. There's the intermediate square, which is used when you do a swap. And there's a two square, which is the final position that your piece will end up in. So if you're not doing a swap, then the intermediate and from should be the same. But if you are doing a swap, then there's some skipping that happens.

At each turn, you need to see what moves you could possibly make. And in move gen, which is one of the files in the handout, we generate all the moves, given a position, depending on whose turn it is. So depending on whose turn it is, you can make different moves.

And in the reference implantation, we iterate through the entire board. And once we find a piece, we generate all the moves from that piece. You can also debug using move generation.

So there's something called perft, which is a debugging function that enumerates all moves at a certain depth. So use perft to make sure that if you make changes to the move generation that you're generating the same number of moves. And if you modify the move generated, just make sure that it returns the same, because regardless of what optimizations you do, you still should see the same moves from each position that you can possibly make.

OK, so now that we talked about move generation, I'll talk about how you tell that a move is good. And for that, we use something called static evaluation. So we use static evaluation to determine which positions are better than others, and which moves that we should make.

And the function eval, which is in eval.c, generate a score based on a position, using some heuristics. And at first, we suggest, instead of making up your own heuristics, we suggest focusing on optimizing the existing structs and evaluation heuristics before coming up with new ones, because it's kind of hard to come up with new ones. And there's a lot of optimizations that you can make to the existing ones.

So I've just grouped these into categories. So there's a few regarding the king. So there's one called KFACE, which is a bonus for your king facing the enemy king. There's KAGGRESSIVE, which gives you a bonus for if your King is closer to the center of the board. And there's MOBILITY, which counts up, basically, how many squares around your king are free. You want to be able to move your king freely.

And there's some regarding pawns. So there's PCENTRAL, which gives you a bonus if your pawns are in the center of the board. And there's PBETWEEN, which basically draw a bounding box with both kings at the corner. And then you count how many pawns are in the center of those.

And then there's points based on distance. So there's LCOVERAGE, which means laser coverage, which is basically you make all the possible moves that you can make from your position. And then you draw the laser path. And then you do some scaling to determine how well you can possibly cover the board, based on your current position. So that's basically how you tell if a position is good or not, with these heuristics.

So I'll just go through the high level of how you actually play the game using search. So at the very highest level, there's something called game search trees, which is we've invented in search.c. But, basically, this is a representation of how you play the game. At the top, there's an orange square, which is the orange side, which is the opening position, and then the arrows.

So the top square-- actually, all the nodes are positions in the tree. And you use move generation that I just talked about, to enumerate all the possible moves from a single position. And each edge is a move.

So to get from position to position, you do moves. And you can see that circle is the position after you've made the move. And you do this tree to some depth d. And then you do static evaluation of the leaves.

So this is at a really high level how game playing programs actually play the game. They enumerate all the possible moves. And then they have a position. And then they pick which one is best, based on evaluation.

But you can see that there's a lot of nodes. Like, if you do this naively, there'd be number of moves raised to d, which is a huge number, and too many to generate. So we're going to talk about how you reduce those later.

There's something that you have to do on search series, which is called Quiescence search, which is if you fix your depth-- let's say you fix depth, and then you go down to the leaves, and you just captured a piece. But it's dangerous to just stop there at fixed depth, because maybe if you searched one level deeper, you would see that the opponent would capture your piece.

And so if you do your search, and you see that you capture a piece at the leaves, or your opponent captures the piece at the leaves, we say, that's not quiet. And you keep searching the tree until there are no more captures. So that's called Quiescence search, because you quiet the position. And that's implemented in the search column.

So this is a graph that I generated by doing the reference spot to different depths. And you can see that the Elo increases as you increase the search depth. So you just search the search tree. And so if you optimize your bot to make it faster, you can search deeper, which means that you'll do better.

So next, I'll talk about min-max search, which is a more complex version of searching that can improve the amount of nodes you have to evaluate. So at a high level, there's two players, max and min. And in our example, there's orange and purple.

And orange is a square. And purple is a circle. And the game trees represents all moves from the current position from a given ply, which means depth. And if the leaves, like I said, you play a static evaluation function.

And max chooses the maximum score among its children. And min chooses the minimum score. So one side is trying to maximize, and one side is trying to minimize.

To evaluate the search try, I'll first talk about an algorithm called alpha beta, which is that each search from a node has a window alpha beta. And if the value of the search falls below alpha, the move is not good enough, and you keep searching. And if the value falls within alpha and beta, then you increase your alpha, which is the lower bound, and you keep searching, because you know you can do at least that well.

And if the value of the search falls above beta, than you generate a beta cut off in return. Beta basically means one side is trying to maximize, and one side is trying to minimize. So beta is basically saying, the opponent would never let you do that move, because it'd be too good. So you don't need to keep searching there, because you're not going to get there anyway.

So I'll do an example. Let's say you have this tree. And if max discovered a move that min wouldn't let you do, because it's too good, then max's other children don't need to be searched, which is what a beta cut off is. So you'd start at the root.

And then you go down to the lowest left leaf. And you see that it's three. So you propagate three up. And then you can see that in this sub-tree, you can do at least three.

And then you keep searching your children. And then you see six. And then you say, OK, now you update your alpha value to be six.

Now, you search four. But four is worse than six. So you don't have to do anything. So you first search the leftmost subtree. And then you see the best move that you could possibly make there.

So you propagate six up to the root. And then you search your other subtrees. But now, you have this value of six that you basically use in the other subtrees.

So you look at two. And you see that two is less than six. So you propagate it up.

But now, you look at nine. And you see that nine is greater than six. So you say that this subtree would let purple do nine, which is greater than six. And so that would be too good, because orange would never let purple do that well.

So you don't have to evaluate five anymore. So you cut off five. Does that make sense?

OK, so, basically, now you apply the same thing to the regular subtree. And you look at seven. And you see that seven is greater than six.

So you propagate that up. And now you're done, because seven is greater than six. So you don't have to search the rest of the subtree. So that's how you evaluate fewer moves than the entire tree.

And there's a theorem that says for a game tree with branching factor b and depth d, and alpha beta search with moves searched in best-first order examines exactly b raised to the d over 2, plus b raised to the d over 2 minus 1 nodes apply d. So best first order means that you sorted the moves in terms of your static evaluation.

The naive algorithm examines b to the d nodes. And in the example I did, you can see how you prune. And for the same work, the search stuff is doubled. And for the same depth, the work is square rooted.

So this is a huge benefit over the naive evaluation. Is everyone good on alpha beta? Great, so the code is pretty short. So I'll just go through some pseudocode for it.

Basically, the main point is that at line 11, one side is trying to minimize and one side is trying to maximize. But if you negate, then that's just the same as minimizing and maximizing. And you get all the possible moves that you could possibly make using gen moves.

And you go through the entire move list. And then you make each of the children. And you search for the score. And then you see whether you had a beta cut off. And then you don't need to search the subtree If you did.

So that was basic alpha beta. And we actually implement a variation of alpha beta called principle variation search. And the main idea is that you assume that the first move is the best one. And you run scout search, which is also called zero window search, on the remaining moves to verify that they're worse.

So in this example, you, again, search the most leftmost subtree. And you see that the best you can do in the left-most subtree is three. And you evaluate the ones to the right of it using scout search, which is not a full search.

You're basically assuming that you can do no better than three. And then now you're kind of doing an initial search to see whether or not that's true. And see you see that some of them are-- the one after that is seven. The first one after that is seven. And the one after that in the other subtree is six.

So then you can prune them, because those are better-- because you know already in those subtrees that you can do better than three. So you don't have to keep evaluating them. And you don't have to-- yeah?

AUDIENCE: How do we know the score of the subtree before we evaluate? How can we prune something?

HELEN XU: So you actually had to find seven. Like, zero and eight are there. But you haven't found them yet.

So, basically, if you thought about doing it serially, you do the leftmost subtree, which has 2, 3, and 0. And then you would find seven. And that would be a cut off, because seven is bigger than three. So you're not actually finding zero and eight.

The point is that you wouldn't get to that subtree, because the opponent wouldn't let you get there, because you can do too well. So they would just not let you go down that path. Like, let's say you were purple, and the opponent is orange.

And you want to get 7 and 8. But the opponent can also search that, and see that you would get 7 and 8. So they would prefer you to do something like two or three.

AUDIENCE: So what do you do instead?

HELEN XU: You're not always making the best move that you could possibly do, because-- like, if you just searched without this pruning, and you just picked-- let's say you wanted to make the best move. Like, if you don't take into account the opponent, then you're never going to get to there. So you're basically trying to find a move that the opponent would let you get to that's also good for you, because you switch off. Yes?

AUDIENCE: [INAUDIBLE]

HELEN XU: I guess in this example, you're purple. No, sorry, you're orange, because you're cutting off-- no, you're purple, because you're trying to maximize what you get at the leaves.

AUDIENCE: [INAUDIBLE]

HELEN XU: Yes. The main point of-- sorry.

AUDIENCE: Oh. We're trying to minimize the score.

HELEN XU: Yes. So orange is trying to minimize the score. And purple is trying to maximize the score.

AUDIENCE: So we're cutting that off, you're saying you don't need to search this because we already know they're the same here. So we shouldn't go down this path anyway.

HELEN XU: Does anyone have questions? Does that make sense? Yeah, it's basically exactly as you said.

So there's kind of this balance between one side trying-- both sides are just trying to make-- you're trying to make good moves. But you're also trying to make the opponent make not good moves, if that makes sense. So you're not only searching for your maximum. But you're also searching to minimize the opponent. Good question.

AUDIENCE: [INAUDIBLE]

HELEN XU: Sorry?

AUDIENCE: So we don't want to choose either of those orange ones. We don't want to let--

I think it's OK. I think you can move on.

HELEN XU: Oh, OK. Yes?

AUDIENCE: What if you and your opponent have different reward criteria? Like, you guys evaluate--

HELEN XU: That's OK. It's fine. The actual evaluation, like what number you assign to each position, is not exposed to the opponent. The main point is that, at the end of each move, you pick one. And they can do with it what they want. Like, that may not have been the one they picked. But it's OK.

Sorry, I think you're orange in this one, because the root is orange.

AUDIENCE: [INAUDIBLE]

HELEN XU: So let's start over. So I think that we are orange. So remember that each edge is a move. And each node is a position.

And so you're orange. And you start at the root. And now you, for example, make the move left. And purple now can make moves whatever three after that.

And now, you're orange again. And then you can make moves after that. And now, you evaluate the position after that as a leaf.

And so, basically, you're searching past like the second level of orange. And you are cutting off if you see that you would do better, because you think that purple would never let you get to that orange node right above. Yes?

AUDIENCE: [INAUDIBLE]

HELEN XU: Yeah, I guess that's the score that you, as orange would receive. Yes?

AUDIENCE: [INAUDIBLE]

HELEN XU: You're not trying to give-- it's not so much like you're trying to give purple zero, as you think that purple would not give you seven and eight, because purple would have to go down the left subtree to give you that. Any other questions?

I'm going to move on with the search then, if there are no questions.

[INTERPOSING VOICES]

HELEN XU: Is everyone good? Can I keep going? OK, so just going back to principal variations pruning, the main idea is that you go down the first path on the left side, thinking that that's the best path. And then you're basically doing initial passes through the trees to make sure that your assumption is correct.

And if they're not correct, then you have to search the entire subtree. But if they are correct, then you kind of fail, you early exit. So you search down the left subtree. And you find three in the leftmost subtree.

And now, you search the ones to the right of that. And those are seven and eight. So those produce a cutoff, because seven and eight is higher than three. So you think that purple would not let you get to that subtree.

And now, you do a scout search again on the middle subtree. And then you see that-- you find this first node of each one of those subtrees underneath the middle subtree. And you see that they're all higher than three.

So it turns out that you failed to prove that you can do no better than three. The main point of the scout search is that you assume that your first move that you search is the best you can do. And then you do initial passes to verify that assumption.

And if you search later subtrees, and you find that-- for example, in this one in the middle, they're all higher than threes. So your assumption is not true. So now you have to do a full search of that entire middle subtree. Is that OK? Are there questions?

So once you find that you have to actually search the middle subtree, you can recursively apply scout search. So you have to search the left subtree in the middle. But now, you apply scout search to the lower middle and the lower right. And you do a zero window search there.

And, again, you assume that you can do no better than six. And now, you're trying to verify that you can do better than six. But you actually can. So you have to search them.

And then you apply the same thing again to the subtree. And you see that you can do better than six on the left one. But you do worse than six on the right one.

And you cut off two, because the middle subtree already gave you two. And so you don't have to search that one. So in this example, there were 13 leaves pruned.

And the point of scout search is that you can improve pruning a little bit over alpha beta, and that you process most of the game tree with zero window searches. The main point is that it reduces your work, because you have to process less. Questions?

So now we're going to talk about-- so I kind of glossed over how you order the moves. So the ordering determines which order you explore the subtrees in. Alpha-beta search and principal variation search depend on putting the best moves in the front to trigger an early cut off.

And the main question is, how do we determine moves, which moves are good, without doing static evaluation at every level? Like, for example, we only did static evaluation with the leaves. And we can't get sortable move list, which is a function in search. And sortable move lists, kind of talk about how you populate that later.

As I said before, moves are represented in 128 bits. So you can use it in 32. And to make them sortable, you store a sort key in the upper 32 bits in 64. And then you sort, based on that key. That make sense?

So I'll just go over some search optimizations that you can do. We actually implement these already. So I'm just going to go through them so it's not super confusing when you look at the code.

The most important one is called the transposition table. The main idea in the transposition table is that chess programs often encounter the same positions repeatedly during a search. And you can store those results in a transposition table to avoid unnecessary feature searches. And I've listed where you can find those.

There's something called Zobrist hashing, which is a technique for hashing a board position which you use to index the transmission table. And it's a table of random numbers, indexed by piece, orientation, and square. So each position has a unique hash.

And it produces the hash by exporting all of these random numbers together. And the advantage of Zobrist hashing is that the hash function can be updated incrementally, which is like if you move a position-- if you move a piece, you just xor it out. And then you xor the new one, so you don't have to recompute the hash each time.

So the transposition table saves you a lot of work by preventing you from researching things. And there's also something called the killer move table. So the transposition table is like how you determine how to do sorting at things that are not the leaves, and also the killing moves table.

So the killer moves people stores moves that are really good so that the opponent wouldn't let you go down that path, so you have to keep recomputing the same values. And the table is indexed by ply, because you tend to see the same moves at the same depth. So the killer move table, basically, just stores move that trigger the beta cut off before in your search.

There's a best move table, which is stored at the root of the search. And it is the move that got the maximum score in your evaluation. And the best move table is indexed by color, piece, square, and orientation. And there's a history table in the code. So these are all, basically, just things to help you optimize your search, and produce early cut offs.

And there's something called null-move pruning, which tries to reduce your search space by first not moving, and then doing a shallower search to see if this subtree is worth further exploring. Basically, it says, don't move, and then do a little bit of evaluation. And if you're still doing really well, even if you didn't move in the subtree, then it's not worth exploring, because the opponent would never let you go there, because the position is too good.

There's futility pruning, which explores moves that only have the potential to increase alpha. And it calculates that possibility by adding a futility margin, which is the most you could possibly gain from going there, and then evaluating a little bit. And if the result does not go higher than alpha, then you skip it, because there's no point in even going that way, because it wouldn't increase your alpha.

There's late move reduction, which is after you order the moves at a position, you explore the-- the-- ones in front are likely to be better. So you explore those in higher depth. And then you explore the ones later with shallower depth, because those are less likely to be good.

And some things that you can optimize are implementing a better opening book. I think we have produced a very basic opening book in the handout. But this is something that you can definitely work on, and make better, because it doesn't have many positions in it right now. And the main point of an opening book is that you store the positions at the beginning of the game that you've already pre-computed.

And that saves time and search, and can store results to a higher depth. And the KM75 theorem implies it's better to keep separate opening books than to keep the same opening book for both sides. So opening books are really helpful, because in the beginning, there's a huge number of moves that you could possibly make. And searching those takes a lot of time.

But if you pre-compute them, you can save them for later. And another useful table you can keep is an end game database, which is a table for guiding your chess program through the end game. For end game positions, the distance from the end might be too far to search entirely.

So you can pre-compute them. And then you store who will win, and how far you are from the end of the game. And we've given you a c file that you can implement it in.

OK, so I'll just go through some guidelines, some tips for the project. I was giving links at most of the bottom of the slides for where you can read up more on these topics. But there's a chess programming wiki. The link is there, which has many more pages about reading about chess playing programs.

Just in general, it's a really good idea to test your code often, because it's easy to make a mistake with your optimizations. And it doesn't appear when you search to fixed depth. So if you start up your bot, you can say, like, search to depth 5, for example.

And then it will tell you like how many nodes per seconds you searched. And then I'll tell you the best move at the end of that search. But you should test full games using the auto tester, and the cloud auto tester, and the script server, just to watch your bot to make sure that it doesn't do anything weird.

And the testing methodology, I went through some of it. There's a webgui. There's a Java autotester. There's a cloud autotester.

And you can do node counts, which is basically just counting the number of nodes in the tree that you searched. And there's function comparison testing, which is, if you optimize a function, you should save the old version, and then just compare the results.

PROFESSOR: Let me make a comment about testing. I can't tell you how often in this class we've had student groups who discover that they've made a whole bunch of changes. And then there's something wrong with their bot. And they can't get back to a stable place when things were correct.

They discover the problem. But they've made 30 changes. And now, which of those 30 is responsible for the problem? So it's really important to test, and have a good test infrastructure for this project.

If you have a really good test infrastructure, it's really easy to be innovative in the kinds of optimizations that you do, because then you know that what you're doing is right. And then you can make forward progress. Otherwise, you'll find yourself self debugging like crazy, and not being able to find the bugs.

Some other tips are, especially when we get to the parallel part, it's non-deterministic programming. And the reason is because as you're executing you're going to be looking up things in transposition table that you're going to want to share, so that if one branch discovers a value then another branch can use that. So it's really important to be able to turn that off so that you're, for example, able to search without a transposition table to get all the searching stuff right, and be able to turn that on independently.

So that's another really important place to do it. Another thing is that when you do timed searches, the time it takes to do the search will vary. And what you'll end up exploring varies. So as much as possible, you wanted to fix depth searches.

Search to five ply to test something, rather than searching for a minute, or whatever the amount of time is, because when you start searching for time, that's, in fact, what you're going to end up doing. But you can't repeat what just happened if you end up searching for that amount of time again, because the machines are not deterministic. And there may be something else going on that causes the amount of time to be different.

And so, for example, if you're making a change that doesn't affect the logic of the program, it's just strictly an optimization, you should get exactly the same result if you do a five ply search, for example. Shouldn't have changed the five ply search. Just a five ply search should be faster.

And so that's a good way-- as much as possible, you want to check things that are deterministic and so forth. And, really, as I say, I can't emphasize this enough, how having a good test infrastructure, the ability to control turn off non-determinism, the ability to test various parts of this program, this is a pretty big piece of code for a project of this nature. And you'll feel pretty overwhelmed by it to begin with.

Once you settle, you'll discover, it's this wonderful thing, where by the end of the project everybody feels really confident about their ability to handle a decent sized piece of code. But when you first get into it, it's like, oh my goodness. There's move ordering. And there's static evaluation.

And there's the search. And what's going on with that transposition table? Because every one of these things has got cleverness in it. OK, so it's really hard code to deal with. But you guys are going to just fine.

HELEN XU: So this is the eval.c file in the handout. So this in 32 here is the evaluation score. And the main function is called eval. And it takes in a position.

And it outputs two scores, one for white and one for black. And right now, it does-- I guess it does counts of the number of pawns. OK, so I was talking before about, p between and p central, which are you pawn heuristics.

And so basically, right now, it iterates through the entire board. You can see for rank and file are just row and column. And it looks at each square in the iteration. And then it looks at the piece and the color of the piece.

And based on the type of the piece, it does some evaluation. So if it's a pawn, it does the pawn heuristics. If it's a fits king, it does these king heuristics. And otherwise, or both-- or not otherwise, I guess-- yeah, in both cases it'll do-- this is an old version. So it's not there anymore.

But this is laser coverage, which we talked about earlier, which doesn't depend on what piece it is. This is after you iterate through the entire board. And then this isn't here anymore either. But we can look at each of these in depth.

So right now, for example, there's p between, which goes through every single pawn in your iteration. And then it will determine whether or not it's between both kings, and the return slide. So it will add it to the score, if you find that it's true.

And there's p central, which takes in a rank and a file. And, basically, it increments something, or it gives you a bonus, depending on how close you are to the center of the board. So look at this. There's a board with-- and F as your file. And R is your rank.

PROFESSOR: I think you have a slightly older version.

HELEN XU: Potentially.

PROFESSOR: It's correct on the screen.

HELEN XU: Is correct in this one?

AUDIENCE: Yeah.

HELEN XU: OK, so this is just the-- I guess is the most updated version. The first one is p central. So this just count the difference between where you are and the center of the board. And it gives you some bonus, depending on how far you are from the center.

And this one is between. Yeah, so this is between, which is a helper for p between. And it tells you whether or not your pawn is in the bounding box determined by the kings. And this one is k face, which is given a king, you look at its orientation. And then you give it a bonus, depending on which way you're facing, and how far you are from the center, I think-- no, how far you are from the opponent.

So f and r where you are. And now it does the delta between you and the opposing king. And then you do some scaling, depending on which direction you're facing. So this is just your orientation.

And then this is k aggressive, which gives you a bonus for how far you are from the edge of the board. So you can see here op square is where do the opposing king is. And delta file and delta rank are how far you are from the opposing king.

And then you add the bonus, depending on which case the deltas fall into. And this gives you a bonus if you're farther from the edge of the board. Yeah, and there's l coverage, which is the most complicated one, probably.

And, basically, what laser coverage does is that, basically, it takes a position. And depending on what side you are, it generates all the moves that you could possibly make from that position. So you generate all with color, which means that, given your color, you generate all the possible moves that you can make.

And you get a list of moves. And you iterate through it. And then you make each of them. And you draw a laser path.

And what the laser path does is, basically, it bounces off some pause. And for each square, you increment the distance, basically, along the path. And if it takes the minimum distance over all these possible paths for each square. And if it doesn't touch a square, then it's just 0.

And it divides it. I can go into this. So it draws the path through this while true. Or this is just changing the orientation if you need to bounce off a pawn.

But this one is setting the-- you keep a laser map. And you keep the minimum path of a laser that would possibly touch that. And, no, this is just changing the orientation.

So then you generate this map for all the possible moves that you could do. And then you do some scaling. So, depending on the distance from the opposing king, you iterate through the entire board.

And you divide the minimum distance by the actual distance from the laser. So the maximum that this ratio can be is 1. And then you multiply it by 1 over the distance.

So this one is really complicated. And there's a lot to optimize here. For example, you probably don't have to iterate through the entire board each time, because even in eval, like here, you have to iterate through the entire board to find each piece. And if you start a better representation, you might not have to do that, like if you just kept track of where the pawns were, because you already keep track of the king separately. So that's one thing you can do.

PROFESSOR: There are two basic strategies for changing the representation of the board. And maybe there are more. But the two basic ones are, instead of keeping the whole board with a piece on each square, and then having to go and search for where the pieces are, you can keep just a list of where the pawns are, and what the locations of the kings are, so that when you want to make a move, you can just go through where they are, rather than having to search through all 64 squares on the board.

Then the other strategy that you can do is use what's called bit boards, where you have a 64-bit word for which, if there's a pawn in a given position, you set that bit. And so there are different ways of representing things that could possibly be, definitely be, more efficient. But you have some choices there.

And also, one of the complexities of this is that to change the representation, there's going to be places in the code you need to find out where they're assuming that things are. So you say, oh, I'll change the board representation. Oh, I didn't realize that over here, there's another place that it's using the board representation, and so forth.

A good strategy for changing board representation is to actually keep both representations around while you migrate functionality from the old one to the new one. And then the advantage of that is that you can actually then use assertions to say, you know, the old one and the new one are the same. So implementing conversion functions is really good.

For example, if you decide you're going to use a bit board representation, have a function that converts the bit board to the standard board so that then you can compare whether you've got the same thing. And, eventually, you'll want to get rid of that.

And, of course, that'll slow down you down, because you're doing more things. But it will allow you to get it correct with a new representation. And once you've got it correct with a new representation with the old one gone, that's when you have a chance to make things go fast.

But it kind of is taking two steps backwards to take five steps forward. I say not one step and two steps, because really, often, you really are slowing things down considerably in order to convert from one representation to another. The most important thing is you maintain the invariant of correctness in your code. You do not want to make something that goes faster, but is wrong, and have to debug the correctness.

You'd much rather ensure that things are correct, are moving to the place that you want to do it. And then you can optimize for performance. So the most important thing is keep that invariant of correctness. And that's where the testing and so forth comes in, having good test infrastructure, and having assertions littered throughout your code.

HELEN XU: And then we can go through the [INAUDIBLE]. Actually, OK, so, just as an example of how you would possibly, one way of determining whether or not you state correct-- so this is an example of a place where I compiled the code. See the binary code is called Lesierchess.

And if you look at help, it gives you some options for what you can do. For example, there's display. And that's the opening position. And let's say I want to search.

So I do a fixed depth, and go depth three. And it tells me the number of nodes that I searched at each depth. And so if you make changes, if they are deterministic, these node counts should stay the same.

So that's one way of telling. So you should keep track of this, and make sure that they're the same. And also, you can do perft, which gives you the number of possible moves you can make. And that should be the same, no matter what you do.

So that's one way of testing. There's other ways. So if you go to higher depth, you'll get more node counts. And here, this is nodes that you searched at this depth. And this is nodes per second. So you want to make this one faster.

So that's how you run the code. And I was supposed to do a demo for the auto tester. So let's say I wanted to do-- so when I made it, it's in a binary called Lesierchess.

And then here, you can type in commands. So you're basically just typing commands from this. Like, you run your binary.

PROFESSOR: This is the UCI interface that we talked about. And in Lesierchess.c is the implementation of that. And so if you want to add your commands to it to help debug, you can enter-- if we go into Lesierchess.c, you can see the table.

What I want to do is show the table of all the options, which is-- there we go, OK.

HELEN XU: This is just the heuristics.

PROFESSOR: So these are tables of heuristics and so forth, which allow you to set the values of the various things, and to say, how much is this heuristic worth to the static evaluation? And through these, all these can be set, so you don't have to recompile the binary if you want to try out things with different-- if you want to auto test with, let me count this as worth a third of a pawn. Let me count this as worth half a pawn, or whatever.

You can just enter it through the UCI interface. And in the auto tester, you can specify that. So it will just test those without you having to recompile binaries for every one of them.

And so there's a table here which basically says, what's the name of the heuristic? What's the variable that is going to be set what the default value is? And pawn ev value is the value of a pawn.

And if there's any restrictions on the range of those values, what's the smallest it can be? What's the largest it can be? So you can edit this table, and so forth. And as I say, you can set it through the UCI interface.

So it's really a very flexible way of getting access to anything that you want to do. You can put your own commands in there, including new heuristics, or whatever. And there's some things in there.

For example, if we go to the other part where they actually are passing the UCI stuff, so it basically takes it. It parses it, figures out what the command is, and then implements the command. So all that kind of stuff, you have control over. So that that will help you in choosing to do other things.

So, for example, if you search for perft or something in there-- so if you have perft, here's what the correct outputs should be. And now, here's the code that it executes. And perft is in a different file. I think it's in the move generation file.

HELEN XU: Do I have the wrong output?

PROFESSOR: That may be for the older game, yeah. I actually noticed a couple of other bugs in there that hadn't been fixed. So we will make sure that those are-- basically, it's just dead code, is what's in there. We need to clean up some of the dead code. Some of the code is from last year. And we changed the game. And not all the dead code got eliminated.

HELEN XU: That'll be fixed for when I make the repost.

PROFESSOR: Yeah. So we're just finishing up some-- right now, I think it's all cleanliness. But if you find any bugs like that, let us know. We'll fix them, and so forth.

Appreciate if you do see other inconsistencies, or what have you. Good, so great project, this is like lots of fun. Next month is going to be lots of fun for all of you. You may not think it's fun every minute of the day. But you'll have a good time. It is fun.