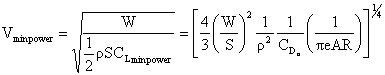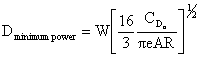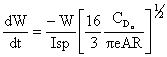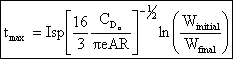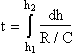IV.  Aircraft Performance
In this lecture we will make the connections between aircraft performance
and propulsion system performance.
For a vehicle in steady, level flight, the thrust force is equal to the drag
force, and lift is equal to weight. Any thrust available in excess of that
required to overcome the drag can be applied to accelerate the vehicle (increasing
kinetic energy) or to cause the vehicle to climb (increasing potential energy).
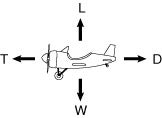
Figure 4.1 Force balance for
aircraft in steady level flight.
Q14 (PDF)
A. Â
Vehicle Drag
Recall from fluids that drag takes the form shown below, being composed of
a part termed parasitic drag that increases with the square of the
flight velocity, and a part called induced drag, or drag due to lift,
that decreases in proportion to the inverse of the flight velocity.
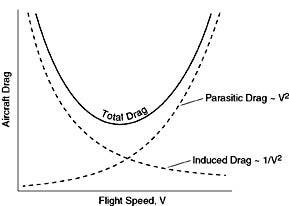
Figure 4.2 Components of vehicle
drag.
Â
                       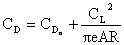                Â
where Â
               Â
where  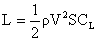 Â
and Â
Â
and  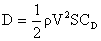
Thus
                       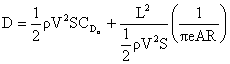               or
              or
                       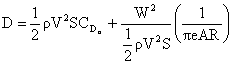
The minimum drag is a condition of interest. We can see that for
a given weight, it occurs at the condition of maximum lift-to-drag ratio
                       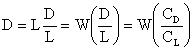
We can find a relationship for the maximum lift-to-drag ratio by setting
                       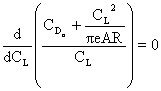
from which we find that
                       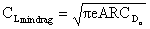          Â
and     Â
         Â
and      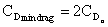
                       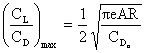           Â
and                             Â
          Â
and                             Â
                      Â
                       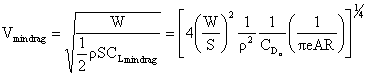
Â
B. Â
Power Required
Now we can look at the propulsion system requirements to maintain steady
level flight since
                       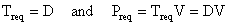
                       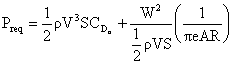
Thus the power required (for steady level flight) takes the form
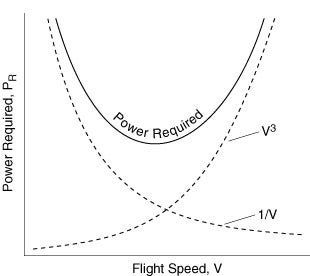
Figure 4.3 Typical power required
curve for an aircraft.
Â
The velocity for minimum power is obtained by taking the derivative of the
equation for Preq with respect to V and setting it equal to zero.
                       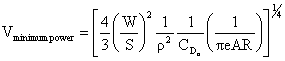
As we will see shortly, maximum endurance (time aloft) occurs when
the minimum power is used to maintain steady level flight. Maximum range
(distance traveled) is obtained when the aircraft is flown at the most aerodynamically
efficient condition (maximum CL/CD).
Homework P4 (PDF)
To see the implications of excess
power, visit NASA Glenn - GO!
|
Â
C. Aircraft Range, the Breguet
Range Equation
Again, for steady, level flight,
                       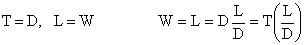
                      Â
The weight of the aircraft changes in response to the fuel burned
                       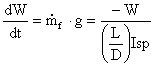
or
                       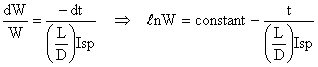
applying the initial conditions,   at   t = 0        W = Winitial      Â
\Â const. = ln Winitial
                       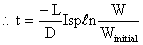
the time the aircraft has flown corresponds to the amount of fuel burned,
therefore
                       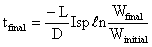
then multiplying by the flight velocity we arrive at the Breguet Range
Equation which applies for situations where Isp and flight velocity are
constant over the flight.
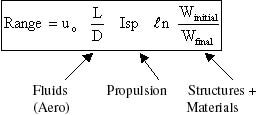
This can be re-written in other forms:
                       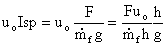
                       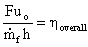 Â
      where      Â
Â
      where       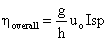
                       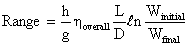           Â
or       Â
          Â
or        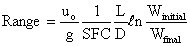
Â
NASA Glenn has a great interactive
Java program for aircraft range - GO!
|
Â
D. Aircraft Endurance
For a given amount of available fuel energy (Joules), the maximum endurance
(time aloft) is obtained at a flight condition corresponding to the minimum
rate of energy expenditure (Joules/second), or Preqmin, as shown
in Figure 4.3.
We can determine the aerodynamic configuration which provides the minimum
energy expenditure:
                       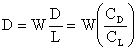             Â
so       Â
            Â
so        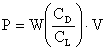
where
                       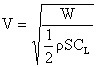
Then
                       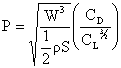
So the minimum power required (maximum endurance) occurs when 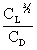 Â is
a maximum.
 is
a maximum.
With a little algebra we can arrive at an expression for the maximum endurance. Setting
                       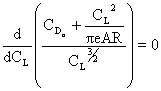
we find that
                       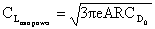        Â
and     Â
       Â
and      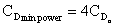
                              and
      and
                       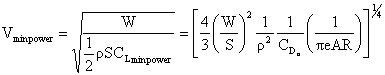
                      Â
Thus the minimum power (maximum endurance) condition occurs at a speed which
is 3-1/4 = 76% of the minimum drag (maximum range) condition. The corresponding lift-to-drag ratio is 86.6% of the maximum lift-to-drag
ratio.
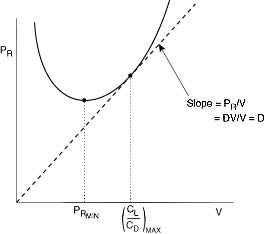
Figure 4.4 Relationship between
condition for maximum endurance and maximum range.
Â
Continuing
                       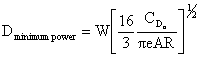
which can be substituted into
                       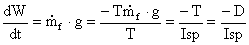
Such that, for maximum endurance
                       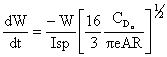
which can be integrated (assuming constant Isp) to yield
                       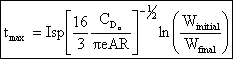
Â
Have some interactive endurance fun at
NASA Glenn - GO!
|
Â
E. Â
Climbing Flight
Any excess in power beyond that required to overcome drag will cause the
vehicle increase kinetic or potential energy. We consider this case by resolving
forces about the direction of flight and equating these with accelerations.
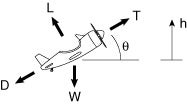
Figure 4.5 Force balance for
an aircraft in climbing flight.
Â
                       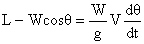           Â
where Â
          Â
where  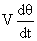  is the accel. normal to the flight path
 is the accel. normal to the flight path
                       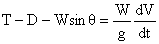        where
       where 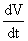  is
the accel. tangent to the flight path
 is
the accel. tangent to the flight path
So the change in height of the vehicle (the rate of climb, R/C)
is:
                       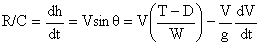
which is instructive to rewrite in the form
                       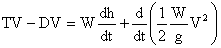
or
                       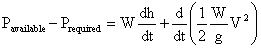
in words:
                       excess power = change in potential energy + change
in kinetic energy
Q15 (PDF)
For steady climbing flight,
                       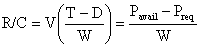
and the time-to-climb is
                       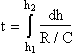
where
                       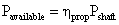       Â
for example, and       Â
      Â
for example, and        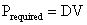
The power available is a function of the propulsion system, the flight velocity,
altitude, etc. Typically it takes a form such as that shown in Figure 4.6. The shortest time-to-climb occurs at the flight velocity where Pavail  Preq is a maximum.
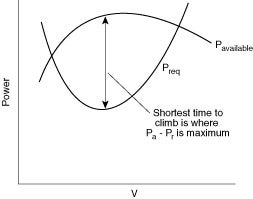
Figure 4.6 Typical behavior
of power available as a function of flight velocity.
Â
Homework P5 (PDF)
To see more on climbing flight, visit NASA
Glenn - GO!
|
Â

![]()

![]() Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â
where Â
               Â
where  ![]() Â
and Â
Â
and  ![]()
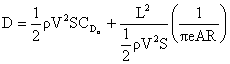 Â Â Â Â Â Â Â Â Â Â Â Â Â Â or
              or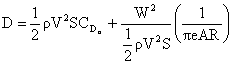
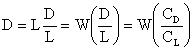

![]() Â Â Â Â Â Â Â Â Â Â
and     Â
         Â
and      ![]()
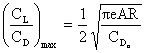 Â Â Â Â Â Â Â Â Â Â Â
and                             Â
          Â
and                              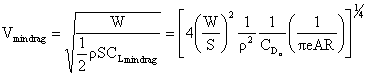
![]()
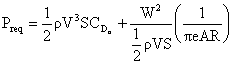

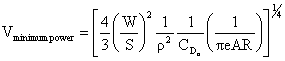
![]()
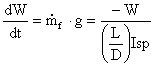
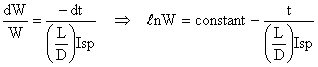
![]()
![]()

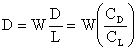 Â Â Â Â Â Â Â Â Â Â Â Â Â
so       Â
            Â
so        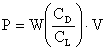
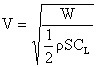
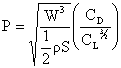
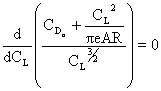
 Â Â Â Â Â Â and
      and